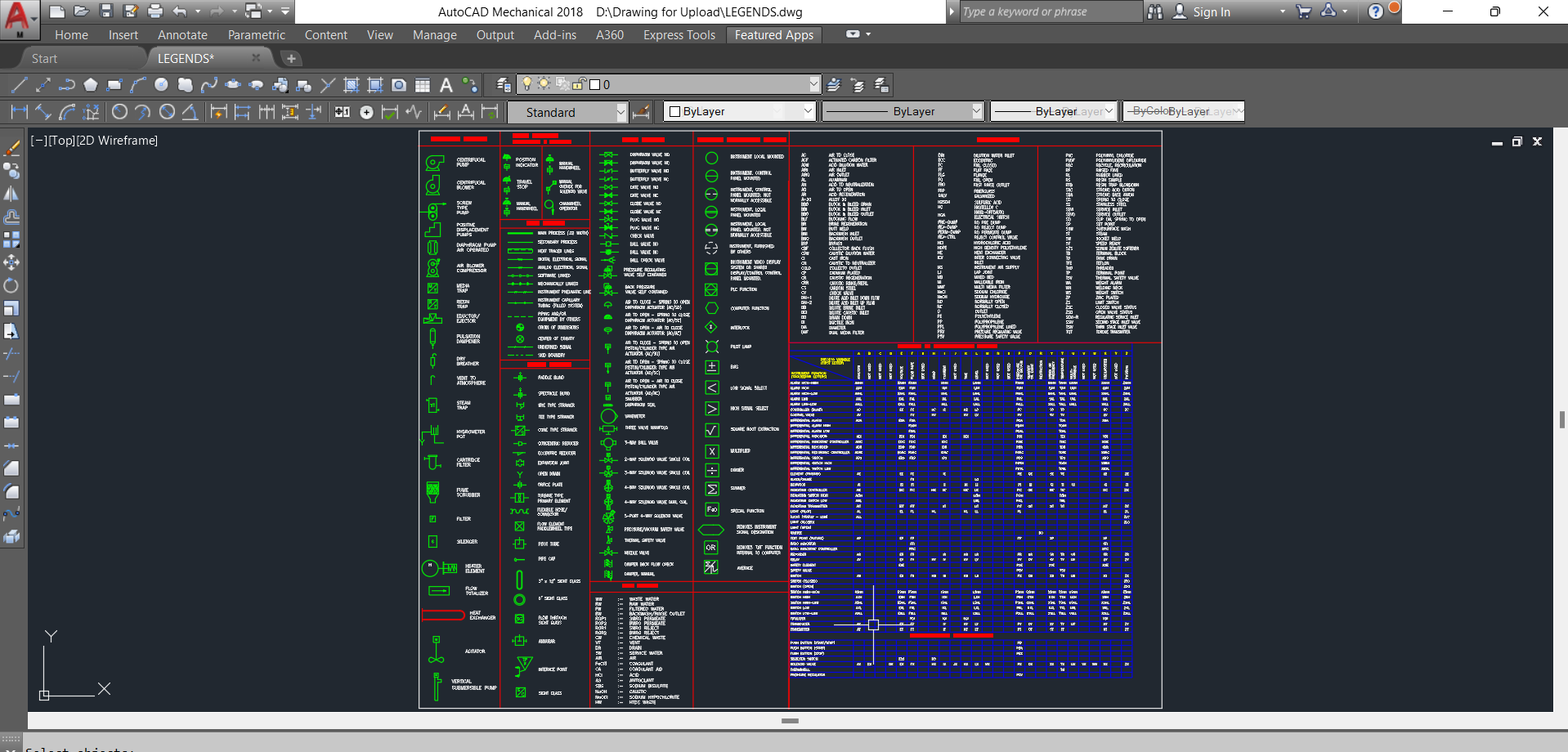
Geometric Constructions DWG Block for AutoCAD

Geometric Constructions DWG Block for AutoCAD

Geometric figures in autocad

Drawing labels, details, and other text information extracted from the CAD file (Translated from Spanish):

Epicycloid epicycloid is the curve generated by the trajectory of a point of a circumference that rolls without sliding on the outside of another guideline circumference. We draw both circumferences tangentially. Center of the center of the we divide the generating circle in equal parts in this is calculated the central angle of the base circumference according to the formula where is the radius of the generatrix the radius of the guideline. We divide an angle of the guideline equal to that found in the same quantity of parts. Defining the points on the circumference we draw lines from the previous points. We draw an arc of length with center in which cut the previous lines in which they will be the successive centers that will occupy the generating circumference. By the points dividing the tracing arcs with center in which they will cut auxiliary circumferences in points that will determine the epicycle. With centers in tracing the mentioned auxiliary circumferences. In the following way we will find the points of the epicycloid: the circumference with center in the intersects with the arc plus the circumference with center in with the one so that it intersects with the outer one more then we go inwards again until of that way we have the points Which by joining them form the epicycloid., Ovoid given the non-symmetric axis we take this axis as diameter of a circle of center of we draw a perpendicular that cuts the circumference in touching this point we draw two lines the points will be centers of the arcs of radius ab respectively. With which we conclude the construction of the desired ovoid., Hypocycloid Hypocycloid is a curve described by a point on a circle that rolls without through the inside of another circumference. Construction given the circumferences generatriz guideline q. The generatrix circumference has in this particular case a third of the radius of the guideline circumference q. The generatrix circumference is divided into several parts because they are located on the circumference giving parts that will have hypocycloids. With center in it are described circumferences with centric that pass by the divisions of the circumference as well as by its center the end of the diameter ab. The radii that cut the circumference of radius at the points respectively are drawn. From these points with radius ob are described arcs that cut the concentric circles described from the points that are the points through which the hypocycloids pass., Ovalo the oval is a crushed circle that resembles an ovoid shape its shape does not deviate much from that of a circumference one usually have one two axes of symmetry. Construct draw an axis trace the perpendicular bisector of the ab axis. Determine the points of intersection of the line with the circumference of center diameter ab. Draw the lines of origin in that contain the points that will limit the arcs of circumferences that make up the oval. Draw the arcs of circles that have centers at the points of radius ab. With centers in tracing the arcs of circumferences that spliced ​​with the two already completing the oval., axis, Parabola: to make a parabola we will use the method of projective beams. Given the vertex axis a point in the parabola. Plot the axis locate the vertex the given point. Draw the rectangle pqvr. Divide pq pr into the same number equal parts number from the point p. Tracing the originals that contain the points given by the line pq. Draw lines parallel to the axis that pass through the points on the pr line. The points of intersection of the semirectas with the lines that have with the points numbered with the miso digit determine the points of the parabola. Locate the symmetrical point to the point with respect to the axis repeat the procedure to complete the path., axis, To trace a horizontal axis locate the vertices also a lower top point draw a rectangle this case divide pq pr into a same number of equal parts we enumerate from p. Draw the half-lines from the points divided into pq. Draw the half-lines from the points divided into pr. Joining the points of intersection of the half-faces with it determine the hyperbola. We locate a point p ‘symmetric of respect to the axis to repeat the same procedure to find the other branch of the hyperbola., Involutes is the spiral described by a point of a thread that remains tense. The thread may be wound around a segment of any regular polygon of any circumference. Construction when drawing a line segment. Alternately centering at the ends of the radii starting with the length of the segment continuing with the distances that result each as seen in the figure., Cycloid the cycloid is the generated curve

Raw text data extracted from CAD file:

Epicicloide La epicicloide es la curva generada por la trayectoria de un punto de una circunferencia (generatriz) que rueda sin deslizamiento por el exterior de otra circunferencia directriz. \W3.83708; 1. Dibujamos ambas circunferencias \W3.83708; tangentemente. (“P” centro de la \W3.83708; generatriz, “O” centro de la directriz) \W3.96629; 2. Dividimos la circunferencia generatriz en \W3.96629; partes iguales (8 en este caso). \W3.99157; 3. Se calcula el ángulo central de la \W3.99157; circunferencia base según la formula a = \W3.99157; 360º r/R. \W8.05618; Donde “a” es el ángulo, “r” el radio de la \W8.05618; generatriz y “R” el radio de la directriz. \W4.10955; 4. Dividimos un ángulo de la circunferencia \W4.10955; directriz igual al hallado en la misma \W4.10955; cantidad de partes. Definiendo los puntos \W4.10955; a,b,c,d,e… en la circunferencia \W3.99438; 5. Trazamos rectas desde “O” a los puntos \W3.99438; anteriores. \W3.98315; 6. Trazamos un arco de longitud “OP” con \W3.98315; centro en “O” que corte a las rectas \W3.98315; anteriores en a1, b1, c1, d1, … que serán los \W3.98315; centros sucesivos que ocupará la \W3.98315; circunferencia generatriz. \W3.99987; 7. Por los puntos que dividen a la generatriz, \W3.99987; trazar arcos con centro en “O” que cortarán \W3.99987; a circunferencias auxiliares en puntos que \W3.99987; determinarán la epicicloide. \W4.03638; 8. Con centros en a1, b1, c1,… trazamos las \W4.03638; circunferencias auxiliares mencionadas. \W4.03628; 9. De la siguiente manera encontraremos los \W4.03628; puntos de la epicicloide: \W8.05621; La circunferencia con centro en P la \W8.05621; intersectamos con el arco más interno; la \W8.05621; circunferencia con centro en a1, con el \W8.05621; siguiente, de forma que d1 se intersecte con \W8.05621; el más externo y luego vamos hacia adentro \W8.05621; nuevamente hasta h1. \W3.83657; 10. De esa manera tenemos los puntos E1, E2, \W3.83657; E3,… que uniéndolos forman la epicicloide. P O a b c d e f g h a1 b1 c1 d1 e1 f1 g1 h1 E1 E2 E3 E4 E5 E6 E7 E8 OVOIDE 1. Dado el eje no simétrico AB, tomamos este eje como diámetro de una circunferencia de centro 1 . 2. De 1 trazamos una perpendicular que corta a la circunferencia en 2; tocando este punto trazamos dos rectas A4 y B3. 3. Los puntos A, 2, B serán centros de los arcos B4, 43y A3 de radios AB, 24 y AB respectivamente. 4. Con lo que concluímos la construcción del ovoide deseado. HIPOCICLOIDE La hipocicloide es una curva descrita por un punto de una circunferencia que rueda sin resbalar, por el interior de otra circunferencia. CONSTRUCCIÓN Dadas las circunferencias generatriz O y directriz Q. 1. La circunferencia generatriz O tiene por radio en este caso particular un tercio del radio de la circunferencia directriz Q. 2. Se divide la circunferencia generatriz en varias partes iguales, 6 por ejemplo, que desarrolladas se sitúan sobre la circunferencia directriz, dando 18 partes iguales, o sea que tendremos 3 hipocicloides. 3. Con centro en Q se describen circunferencias con céntricas que pasen por las divisiones 1 (5) y 2 (4) de la circunferencia generatriz, así como por su centro O y el extremo B del diámetro AB. 4. Se trazan los radios Q 1’ , Q 2’ , Q 3’ , Q 4’ , Q 5’. Q 1’’ , Q 2’’ , … y Q 5’’’ que cortan a la circunferencia de radio Q O en los puntos O 1’ , O 2’ , O 3’ … O 5’’’ respectivamente. 5. Desde estos puntos y con radio OB se describen arcos que cortan a las circunferencias concéntricas descritas desde Q en los puntos a, b, c, d, e, f, g, h, i, j, k, l, m, n y p que con los A, 6’ y 6’’ son puntos por los que pasan los hipocicloides. O1' O Q 1 2 3 B 4 5 6 A 1' 2' 3' 4' 5' 6' O2' O3' O4' O5' O6' a b c d e A A 2 1 3 4 1 2 3 4 5 6 7 8 9 10 11 O O1 O2 O3 O4 O5 O6 O7 O8 O9 O10 O11 E A 1' 2' 3' 4' 5' 6' 7' 8' 9' 10' 11' B a b c d e f g h i j k OVALO El óvalo es un círculo aplastado que se asemeja a una forma ovoide o elíptica, su forma no se aparta mucho de la de una circunferencia o una elipse, suelen tener uno o dos ejes de simetría. CONSTRUCCION 1. Dibujar un eje (eje AB). 2. Trazar la mediatriz m del eje AB. 3. Determinar los puntos O1 y O2 de intersección de la recta m con la circunferencia de centro O y diámetro AB. 4. Dibujar las semirrectas de origen en A y en B que contienen a los puntos O1 y O2 respectivamente, las que limitaran los arcos de circunferencias que constituyen el óvalo. 5. Trazar los arcos de circunferencias que tienen centros en los puntos A y B, de radio AB. 6. Con centros en O1 y O2 trazar los arcos de circunferencias que empalman con los dos ya trazados, completando el óvalo. B A O 01 O1 m P Q 1 2 3 3 2 1 Eje R Parábola: Para realizar una parábola haremos uso del método de haces proyectivos. Dado el eje , el vértice y un punto P de la parábola. 1. Trazar el eje e, ubicar el vértice V y el punto P dados. 2. Dibujar el rectángulo PQVR. 3. Dividir PQ y PR en el mismo numero y partes iguales y numerarlos a partir del punto P. 4. Trazar las semirectas de origen V que contienen a los puntos dados por la recta PQ. 5. Trazar rectas paralelas al eje e, que pasen por los puntos situados en la recta PR. 6. Los puntos de intersección de las semirectas con las rectas que tienen con los puntos numerados con el miso digito determinan los puntos de la parábola. 7. Ubicar el punto P’ simétrico al punto P respecto al eje e, y repetir el procedimiento para completar el trazado. V 1 3 3 3 2 2 2 2 1 1 1 1 1 2 2 3 3 3 T R S U A B C D O \fCalibri|b0|i0|c0|p34;\H0.39418x;\LElipse 3 2 1 1 2 3 P Q R V1 V2 P' Q' Eje X \LHipérbola 1) Trazar un eje X horizontal y ubicar los vértices V1 , V2 , y también un punto superior o inferior 2) Dibujar un rectángulo (en este caso PQV1R). 3) Dividir PQ y PR en un mismo número de partes iguales y enumeramos a partir de P. 4) Trazar las semirrectas desde V1 hacia los puntos divididos en PQ. 5) Trazar las semirrectas desde V2 hacia los puntos divididos en PR. 6) Unir los puntos de intersección de las semirrectas con el mismo digito, estos determinan la Hipérbola. 7) Ubicamos un punto P' simétrico de P respecto al eje X, repetir el mismo procedimiento para hallar la otra rama de la Hipérbola. INVOLUTAS Es la espiral descrita por un punto de un hilo que se desarrolla, manteniéndose tenso. El hilo puede estar enrrollado alrededor de un segmento de un polígono regular cualquiera o de una circunferencia. Construcción Cuando se traza de un segmento de recta. * Haciendo centro alternativamente en los extremos del segmento, se trazan radios , empezando con la longitud del segmento y continuando con las distancias que resulten cada vez, como se observe en la figura. Cicloide La cicloide es la curva engendrada por un punto de circunferencia que rueda sin resbalar, a lo largo de una línea recta. \fCalibri|b0|i0|c0|p34;\W5.15642; 1. Dado el diámetro de la \W5.15642; circunferencia generatriz, se divide \W5.15642; el circulo generador O, en varias \W5.15642; partes iguales, 12 por ejemplo. \W5.22102; 2. Sobre una línea recta tangente a la \W5.22102; circunferencia se desarrolla esta de \W5.22102; A a B, siendo esta última recta la \W5.22102; directriz. \W5.23366; 3. La recta AB se divide a su vez en \W5.23366; otras 12 partes iguales. \W5.29265; 4. Por el centro O se traza OE, paralela \W5.29265; a la directriz AB. \W5.23507; 5. Por los puntos 1', 2', 3', 4',… 11', se \W5.23507; levantan perpendiculares a AB, que \W5.23507; cortan a OE en los puntos O1, O2, \W5.23507; O3,…… O11 respectivamente. \W5.22945; 6. Se trazan paralelas a AB por los \W5.22945; puntos de división de la \W5.22945; circunferencia 1(11), 2(10), 3(9), \W5.22945; 4(8), 5(7), 6. \W5.23788; 7. Con el radio del circulo generador, \W5.23788; OA, y desde los centros O1, O2, \W5.23788; O3,…… O11, se describen arcos que \W5.23788; cortan correspondientemente a las \W5.23788; paralelas anteriores en los puntos a, \W5.23788; b, c, d, e, f ,g ,h, i, j, k, por donde \W5.23788; pasa la cicloide.

Language	Spanish
Drawing Type	Block
Category	Drawing with Autocad
Additional Screenshots
File Type	dwg
Materials	Other
Measurement Units
Footprint Area
Building Features	Car Parking Lot
Tags	autocad, block, constructions, DWG, figures, geometric